

Specifically:ĭefinition 1 Let H n be a 2 n-dimensional Hilbert space (n qubits), and let C be a K-dimensional subspace of H n. In general, a quantum error-correcting code is a subspace of a Hilbert space designed so that any of a set of possible errors can be corrected by an appropriate quantum operation.
QUANTUM ERROR CORRECTION OVERHEAD HOW TO
The theory of fault-tolerant quantum computation tells us how to perform operations on states encoded in a quantum error-correcting code without compromising the code's ability to protect against errors. Table 1 shows the overhead required to complete a round of logical operations with error correction for a given number of logical qubits k and code distance d for a number of quantum LDPC codes, specifically, hyperbicycle and hypergraph product codes explicitly constructed in ( 31, 50 ). To build a quantum computer, we face an even more daunting task: If our quantum gates are imperfect, everything we do will add to the error. By adding extra qubits and carefully encoding the quantum state we wish to protect, a quantum system can be insulated to great extent against errors. The theory of quantum error correction quickly evolved producing more and more sophisticated classes such as stabilizer codes, which use ancilla qubits to protect the logical qubit, or. The theory of quantum error-correcting codes has been developed to counteract noise introduced in this way. Any qubit stored unprotected or one transmitted through a communications channel will inevitably come out at least slightly changed.
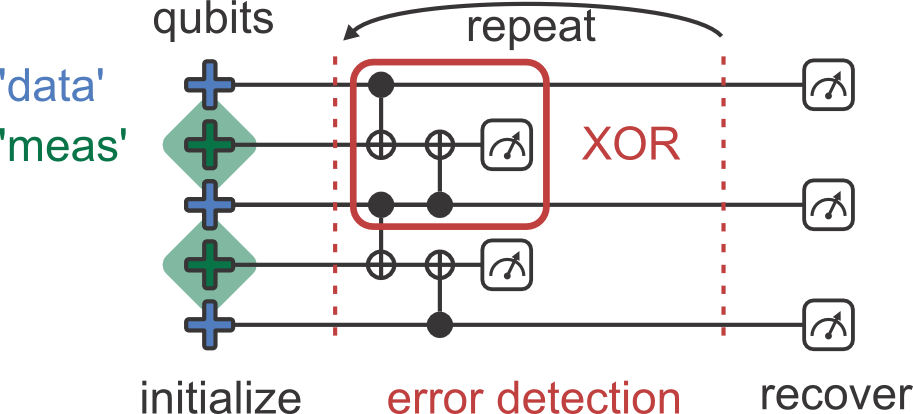
Building a quantum computer or a quantum communications device in the real world means having to deal with errors.


 0 kommentar(er)
0 kommentar(er)
